P3884 [JLOI2009] 二叉树问题

by小儿投稿

来我们看一下问题

给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 x ，y 之间的距离。

深度简单，就是树有多少层呗。

宽度也简单，找到节点数最多的层数的节点树呗。

那这个指定节点x,y之间的距离是什么玩意呢？

请看VCR这句话

宽度表示二叉树上同一层最多的结点个数，节点 u,v 之间的距离表示从 u 到 v 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

怎么理解这句话呢，不如说我们用样例给的8和6做为例子吧

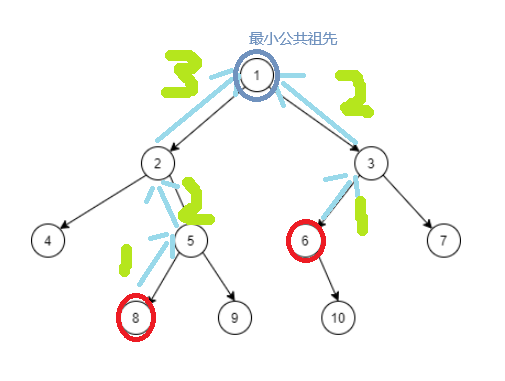
看图，这里8到最小公共祖先的距离为3，6到最小公共祖先的距离为2，那么他们的距离为：

(3*2)+2 = 8

综合起来就是(x*2)+y，那要求得问题解决了，那么最小公共祖先怎么求呢

我们可以将y（x也行）到根节点（注意这里是整棵树的根节点也就是1）中经过的的点全部标记,在让x向根节点走，第一个遇到的被标记的点就是最小公共祖先

最小公共祖先求到了，剩下的会做了吧（别告诉我层数都不会算）

code:

#include<bits/stdc++.h>
using namespace std;
struct node{
    int l,r;
}a[110];
int b[110],vis[110];
int f[110],d[110],ans1,ans2,ans3;
void init(int now,int sum){
    f[now] = sum;
    d[sum]++;
    ans1 = max(ans1,sum);
    ans2 = max(ans2,d[sum]);
    if(a[now].l != -1){
        init(a[now].l,sum+1);
    }
    if(a[now].r != -1){
        init(a[now].r,sum+1);
    }
}

void lca(int now){
    if(now == -1){
        return;
    }
    vis[now] = 1;
    lca(b[now]);
}
int main(){
    memset(a,-1,sizeof(a));
    memset(b,-1,sizeof(b));
    memset(d,0,sizeof(d));
    memset(f,0,sizeof(f));
    memset(vis,0,sizeof(vis));
    int n,p,q;
    cin>> n;
    for(int i = 1;i < n;i++){
        int L,R;
        cin>> L >> R;
        if(a[L].l == -1){
            a[L].l = R;
        }else{
            a[L].r = R;
        }
        b[R] = L;
    }
    cin>> p >> q;
    init(1,1);
    lca(q);
    int t = 0;
    for(int i = p;i != -1;i = b[i]){
        if(vis[i]){
            t = i;
            break;
        }
    }
    ans3 = (f[p]-f[t])*2+(f[q]-f[t]);
    cout<< ans1 << "\n" << ans2 << "\n" << ans3;
    return 0;
}