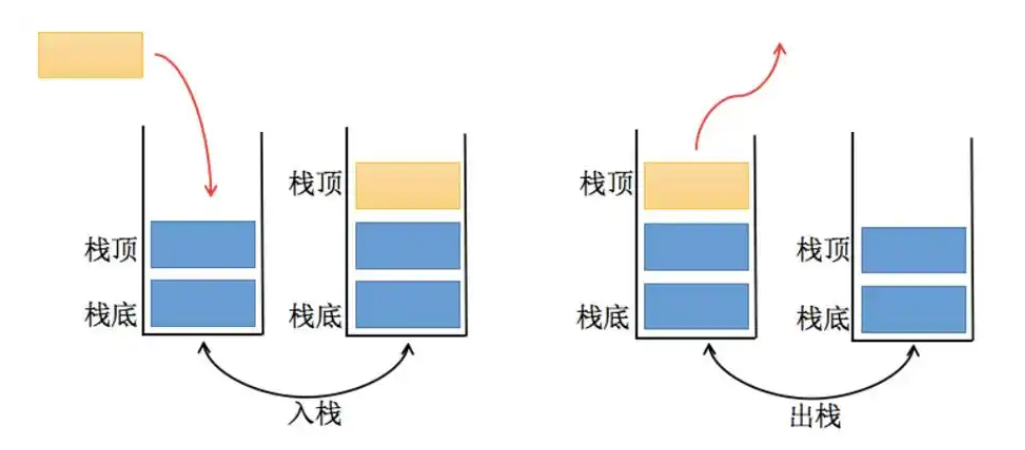
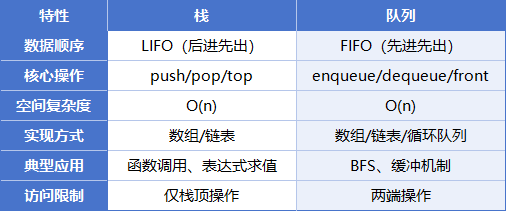
栈(Stack)—— 后进先出的数据容器
栈是一种LIFO(Last In First Out)数据结构,如同自助餐厅的餐盘堆叠,最后放置的盘子总是最先被取用。
妈妈正在烙饼,烙好的会放在上面,这时候你去取,只能取最上面的饼。
核心操作
push():元素入栈(时间复杂度O(1))
pop():栈顶元素出栈(O(1))
top():访问栈顶元素(O(1))
empty():判断栈空(O(1))
size() :查询栈元素数量
C++实现方式
/* 初始化栈 */
stack<int> stack;
/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);
/* 访问栈顶元素 */
int top = stack.top();
/* 元素出栈 */
stack.pop(); // 无返回值
/* 获取栈的长度 */
int size = stack.size();
/* 判断是否为空 */
bool empty = stack.empty();
//访问或操作时,需要先判断栈是否为空栈典型应用场景
函数调用栈(保存返回地址)
撤销操作(Ctrl+Z)
括号匹配校验
表达式求值(后缀表达式)
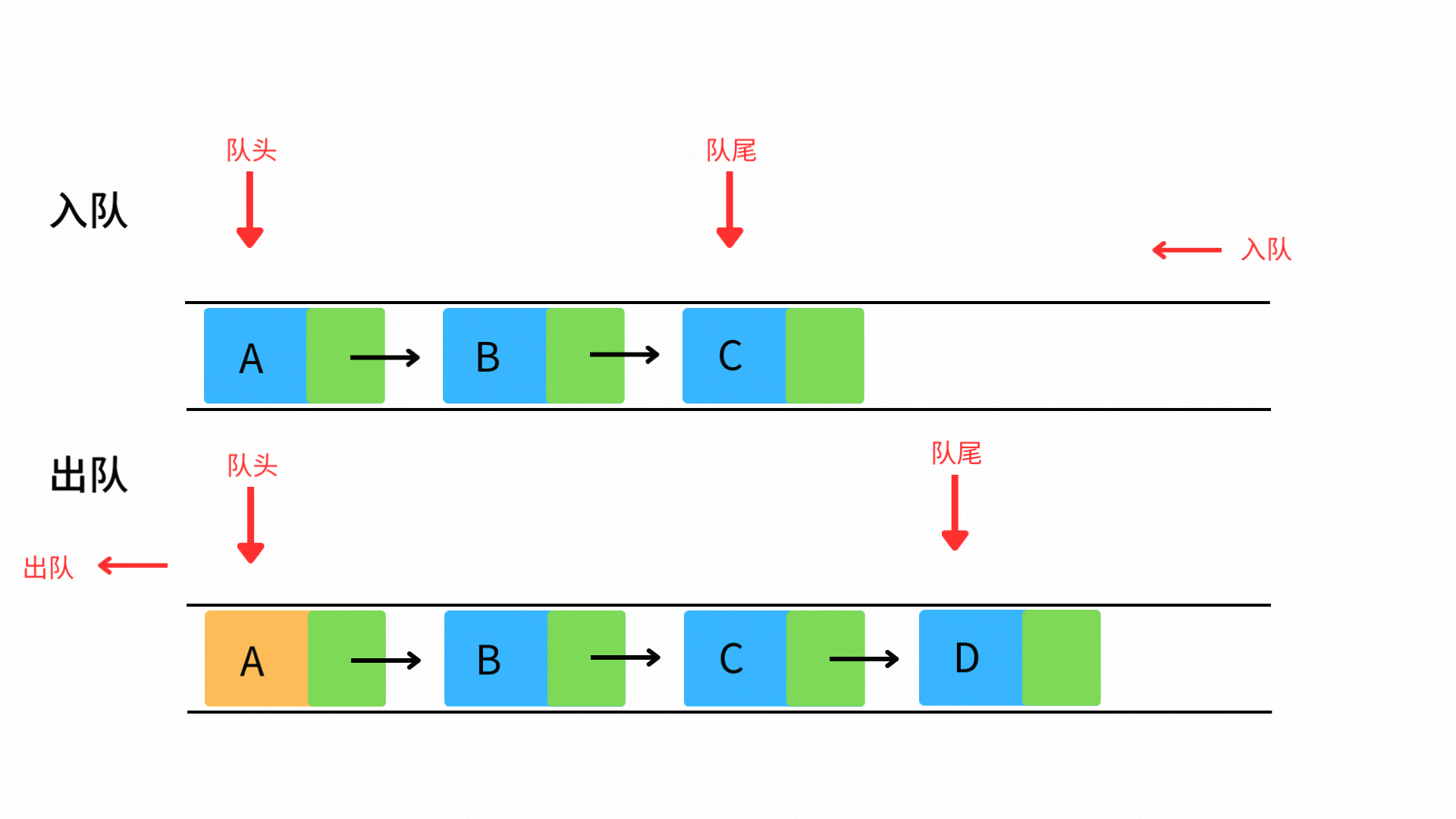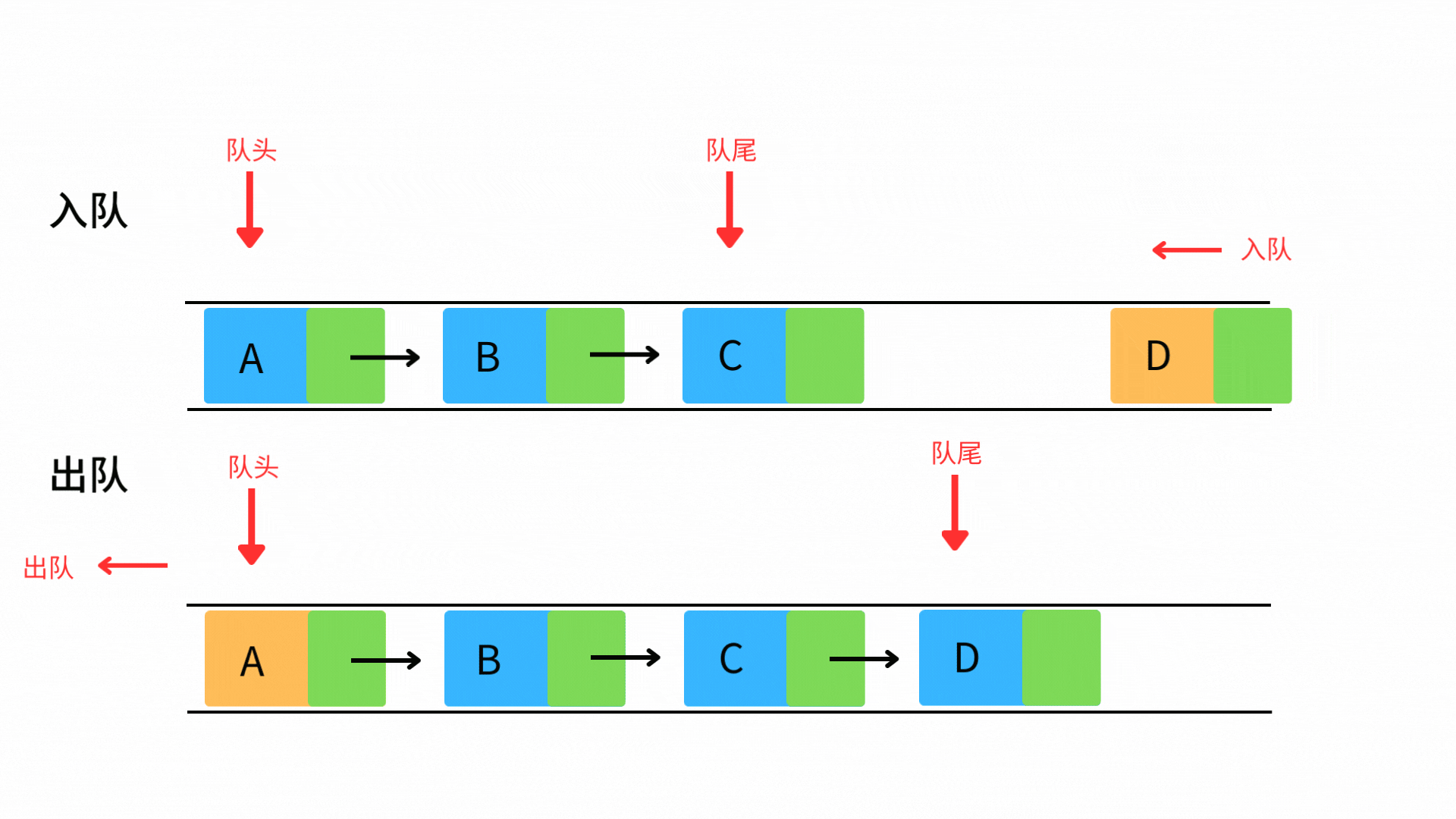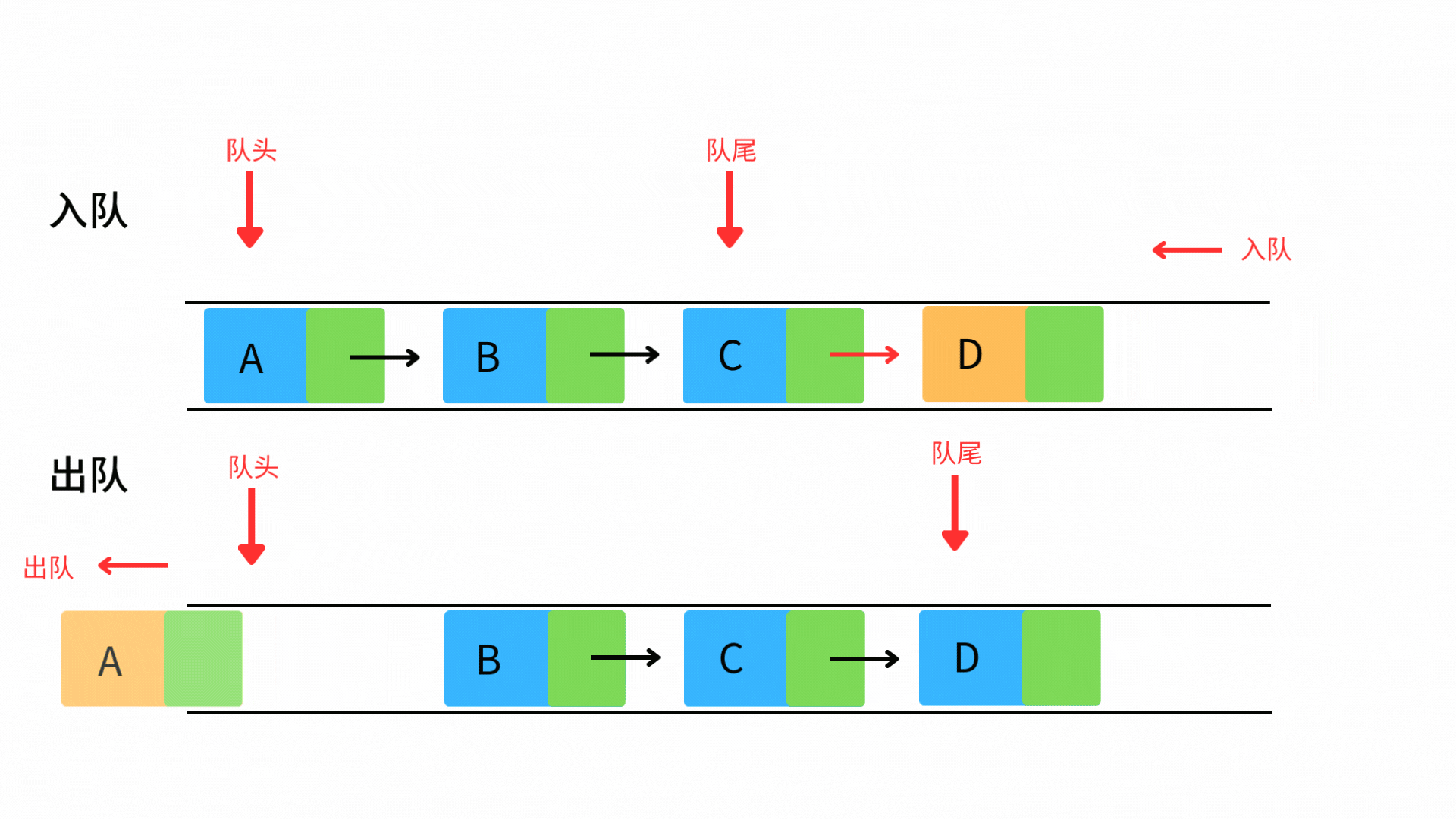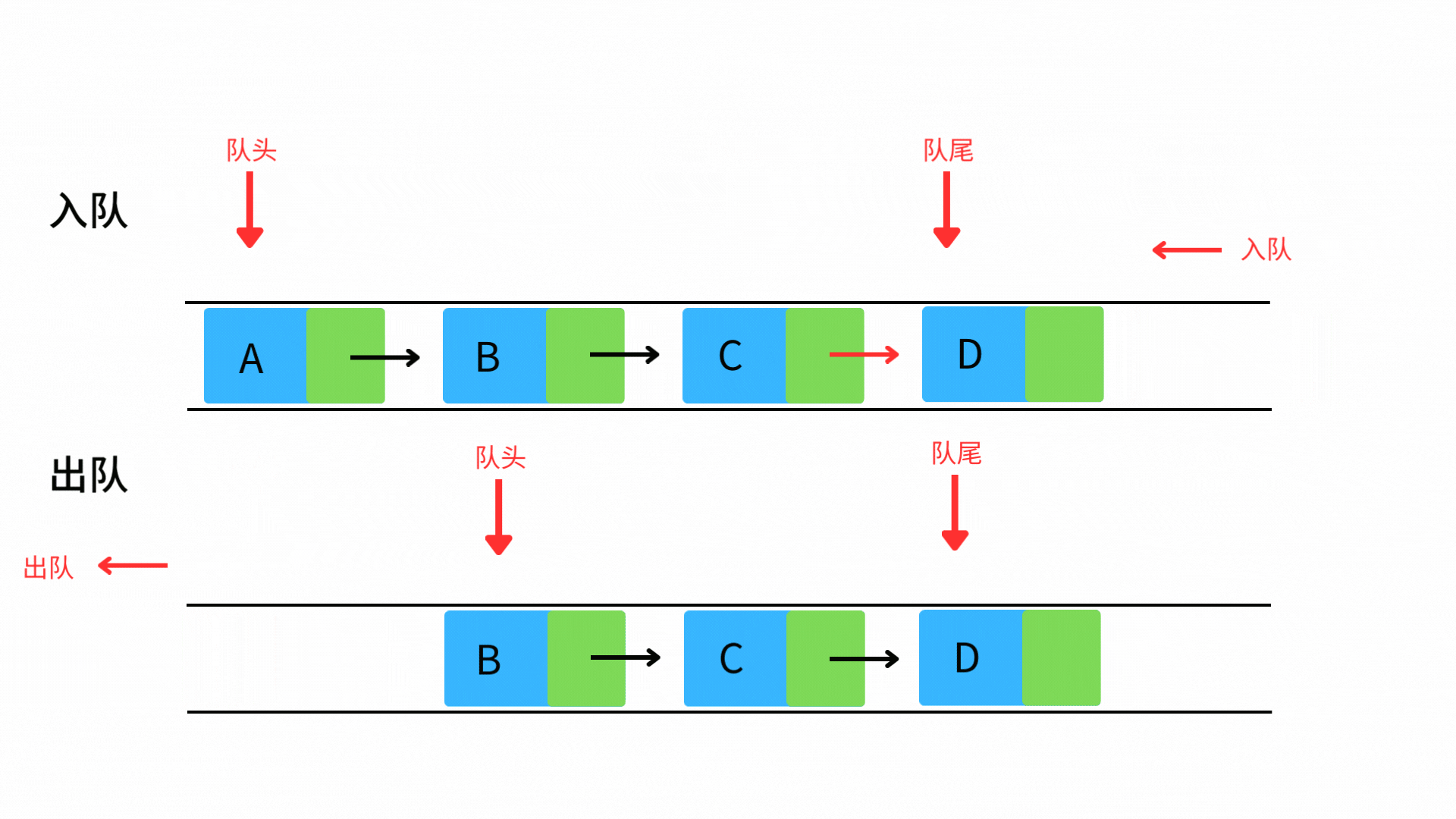
队列(Queue)—— 先进先出的数据通道
队列遵循FIFO(First In First Out)原则,类似超市结账队伍。
妈妈小时候经常教育我们,要礼貌排队,排在前面的人,先买。
核心操作
enqueue():元素入队(O(1))
dequeue():队首出队(O(1))
front():访问队首(O(1))
empty():判断队空(O(1))
C++实现方式
/* 初始化队列 */
queue<int> queue;
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* 访问队首元素 */
int front = queue.front();
/* 元素出队 */
queue.pop();
/* 获取队列的长度 */
int size = queue.size();
/* 判断队列是否为空 */
bool empty = queue.empty();
//操作队列出队时,需要先判断队列是否为空典型应用场景
打印机任务队列
消息队列系统
广度优先搜索(BFS)
多线程任务调度
栈与队列对比分析
添加双向队列
双向队列
在队列中,我们仅能删除头部元素或在尾部添加元素。双向队列(double-ended queue)提供了更高的灵活性,允许在头部和尾部执行元素的添加或删除操作。
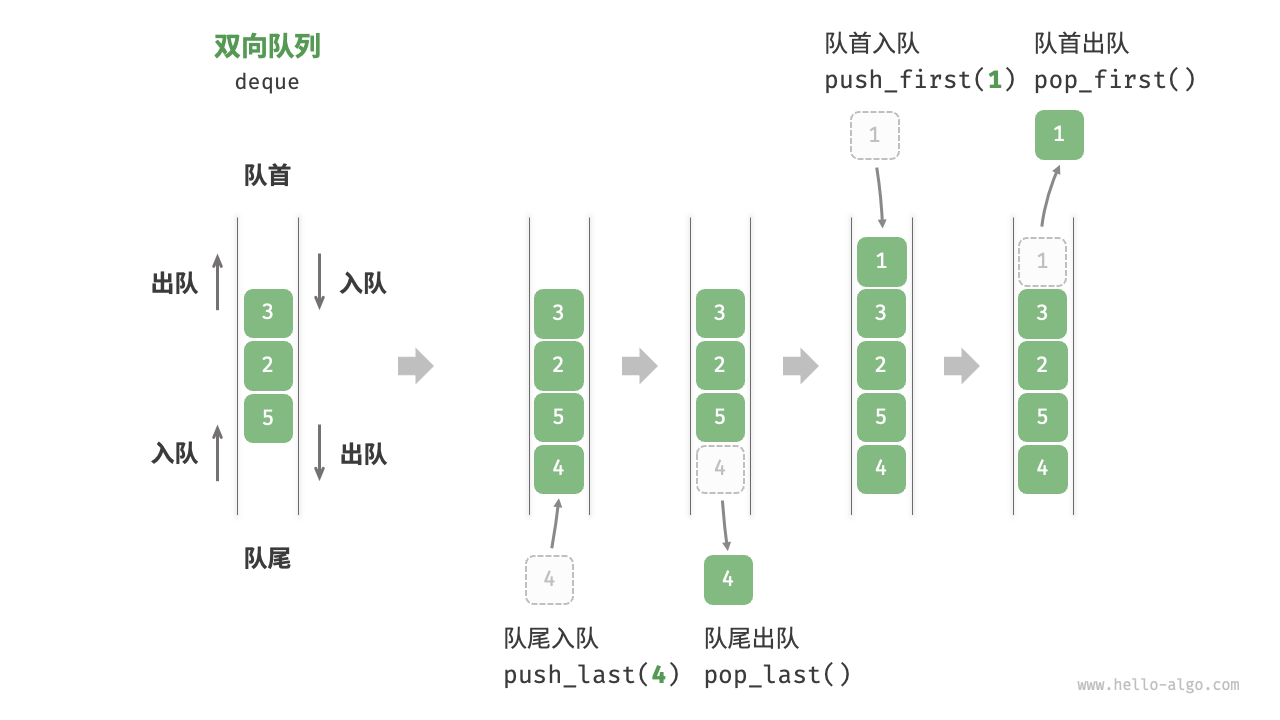
双向队列常用操作
C++实现方式
/* 初始化双向队列 */
deque<int> deque;
/* 元素入队 */
deque.push_back(2); // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3); // 添加至队首
deque.push_front(1);
/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back(); // 队尾元素
/* 元素出队 */
deque.pop_front(); // 队首元素出队
deque.pop_back(); // 队尾元素出队
/* 获取双向队列的长度 */
int size = deque.size();
/* 判断双向队列是否为空 */
bool empty = deque.empty();双向队列应用
双向队列兼具栈与队列的逻辑,因此它可以实现这两者的所有应用场景,同时提供更高的自由度。
我们知道,软件的“撤销”功能通常使用栈来实现:系统将每次更改操作 push 到栈中,然后通过 pop 实现撤销。然而,考虑到系统资源的限制,软件通常会限制撤销的步数(例如仅允许保存 50 步)。当栈的长度超过 50 时,软件需要在栈底(队首)执行删除操作。但栈无法实现该功能,此时就需要使用双向队列来替代栈。请注意,“撤销”的核心逻辑仍然遵循栈的先入后出原则,只是双向队列能够更加灵活地实现一些额外逻辑。
重点回顾
栈是一种遵循先入后出原则的数据结构,可通过数组或链表来实现。
在时间效率方面,栈的数组实现具有较高的平均效率,但在扩容过程中,单次入栈操作的时间复杂度会劣化至 O(n) 。相比之下,栈的链表实现具有更为稳定的效率表现。
在空间效率方面,栈的数组实现可能导致一定程度的空间浪费。但需要注意的是,链表节点所占用的内存空间比数组元素更大。
队列是一种遵循先入先出原则的数据结构,同样可以通过数组或链表来实现。在时间效率和空间效率的对比上,队列的结论与前述栈的结论相似。
双向队列是一种具有更高自由度的队列,它允许在两端进行元素的添加和删除操作。
Q & A
Q:浏览器的前进后退是否是双向链表实现?
栈” 的体现。当用户访问一个新页面时,该页面会被添加到栈顶;当用户点击后退按钮时,该页面会从栈顶弹出。使用双向队列可以方便地实现一些额外操作,这个在“双向队列”章节有提到。
Q:双向队列像是两个栈拼接在了一起,它的用途是什么?
双向队列就像是栈和队列的组合或两个栈拼在了一起。它表现的是栈 + 队列的逻辑,因此可以实现栈与队列的所有应用,并且更加灵活。
Q:撤销(undo)和反撤销(redo)具体是如何实现的?
使用两个栈,栈 A 用于撤销,栈 B 用于反撤销。
每当用户执行一个操作,将这个操作压入栈
A,并清空栈B当用户执行“撤销”时,从栈
A中弹出最近的操作,并将其压入栈B当用户执行“反撤销”时,从栈
B中弹出最近的操作,并将其压入栈A

